In middle school, my friend Paul used to remember the rules for multiplying integers like this:
- If two good people start dating, that is a good thing. A positive person x a positive person = a positive result.
- If a good person and a bad person start dating, that is a bad thing. A positive person x a negative person = a negative result.
- If two bad people start dating… well, I suppose that is good. They deserve each other, and it takes them out of the running for all of us good folks. So, a negative person x a negative person = a positive result for everyone.
As fun as this mnemonic is, as a teacher, I have to ask myself: How do we do better than this? How do we ensure that kids do not simply memorize the rule but actually understand why it works? And how do we do that if most of us adults actually don’t know why it works?
Why DOES a negative times a negative equal a positive?
Representing Multiplication by a Positive Multiplier
Before we answer that question, let’s take a look at some models for the multiplication of positive integers.
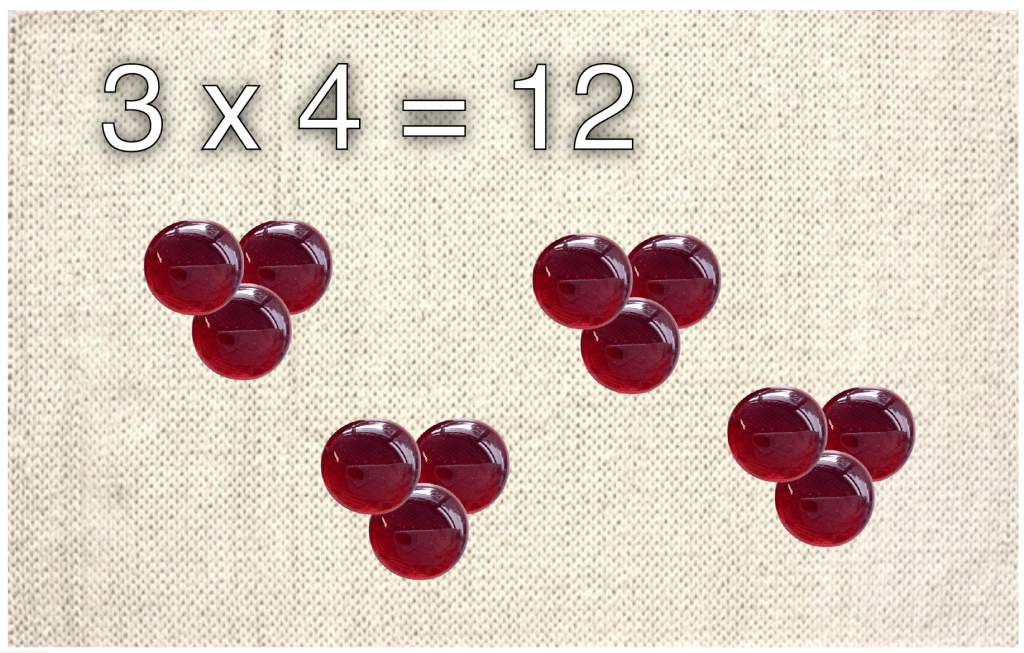
One way to think about multiplication is adding equal groups, or repeated addition. Here we have groups of 3 taken 4 times for total of 12 red gems.
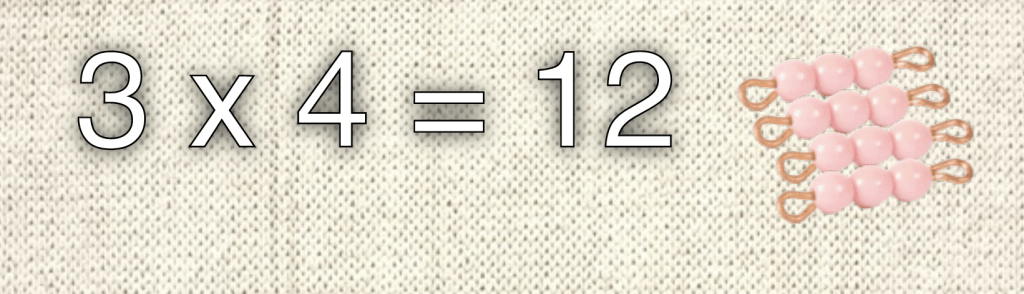
Another way to think of multiplication is as equal rows, represented using bead bars.
These models can easily be adapted to multiply a negative integer by a positive integer. Take a look at two ways to think about -3 x 4 = -12.


Representing Multiplication by a Negative Multiplier
Here is where things get interesting…
How do you adapt these models to represent 3 x -4 = -12? What does it mean to take the number 3 negative four times? Does it mean you take the 3 and discard it? If so, where does the 3 come from if we started with nothing?
Take a look at the model below. If I start with +1 and -1, technically, I am still starting out with a value of zero because they cancel one another out. For children, sometimes it is helpful to visualize these as a positive and a negative charge. Because the value is zero, I can add as many of these Neutral/Zero Pairs as I would like.



Then, it is easy to multiply by a negative multiplier, as I can easily remove groups equal groups from my work space instead of adding them. This works whether the multiplicand is positive or negative.
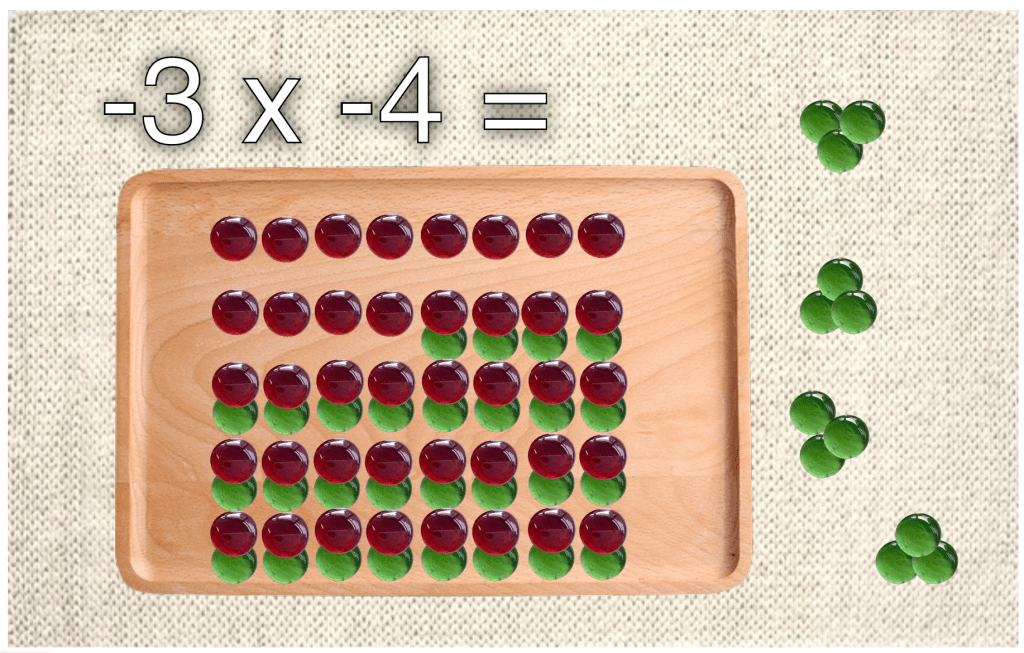
Now we can see why a negative times a negative is a positive! When we remove negative charges from a neutral field, we are left with a positive charge.
For students who prefer to think of multiplication as an area or an array rather than as of equal groups, you can use bead bars in the same way.




Why does this matter?
— Philip D. O’Brien, from the introduction to Psychoarithmetic by Maria Montessori“We have to let children experience the beauty of arithmetic… it is always something to discover and to perceive by the hand before being understood by the mind.”
Maria Montessori was far ahead of her time in that she understood very clearly that children come to learn about and understand the world through their hands. It is one thing to be told how something works; it is quite another to discover why it works on your own. Through mathematical modeling, children can uncover the rule that a “negative times a negative equals a positive” for themselves.
And why shouldn’t they? If we believe that children are fully human, capable of reasoning, why should the children we teach be any less capable of mathematical thought than those who first developed theorems long ago? Unlike language, math was not developed by humans but instead is a way that humans express something that is inherently true. If mathematical laws were able to be uncovered through reasoning in the past, it follows that they can be uncovered through reasoning again and again, discovered afresh by each new generation of thinkers and learners.
— Mario Montessori, Maria Montessori’s Contribution to the Cultivation of the Mathematical Mindi“…the absorption of mathematical knowledge can be natural, easy, and a source of joy; the joy of one who discovers in himself powers that he had not even suspected.”